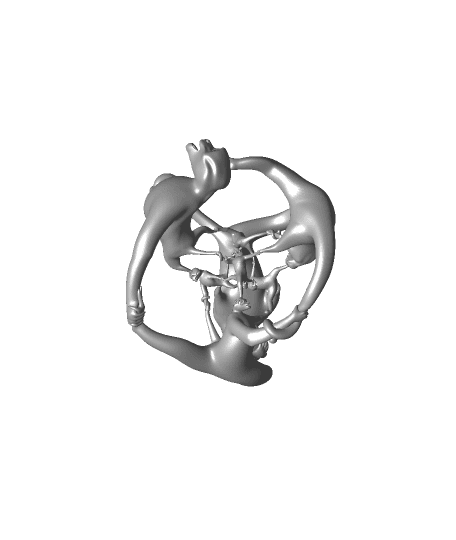Model originally uploaded to Thingiverse at https://www.thingiverse.com/thing:394634.
This model is featured in figure 3.31 of Visualizing Mathematics with 3D Printing.
This sculpture was inspired by a question of Vi Hart. As far as we know, this is the first sculpture (in fact, physical object) with the quaternion group as its symmetry group. The quaternion group {1,i,j,k,-1,-i,-j,-k} is not a subgroup of the symmetries of 3D space, but it is very naturally a subgroup of the symmetries of 4D space. The monkey was designed in a 3D cube, viewed as one of the eight cells of a hypercube. The quaternion group moves the monkey to the other seven cells. Radial projection moves the monkeys onto the 3-sphere, the unit sphere in 4D space, then stereographic projection moves the monkeys to 3D space. The distortion in the sizes of the monkeys comes only from this last step - otherwise all eight monkeys are identical. For more details, see Vi's and my paper, or Evelyn Lamb's blog post at Scientific American.
This is joint work with Will Segerman. Also available from Shapeways.
Also check out the interactive animated online version at monkeys.hypernom.com. (Use the WASD keys, arrow keys, numbers 1-6.)